Annexe V: Prédiction de l’abondance en microplastiques

Random Forest

Source : scikit-learn random forest

criterion : absolute error

La régression avec forêt aléatoire est une technique d’apprentissage automatique (machine learning) utilisée pour prédire des résultats continus (par opposition aux catégories dans la classification). C’est une méthode d’apprentissage ensembliste, ce qui signifie qu’elle combine les prédictions de plusieurs algorithmes d’apprentissage automatique pour produire des prédictions plus précises.

Toutes les conditions

Fréquentation moyenne

Haute fréquentation

Graviers

Sable

Plage seche et sable fins

Plage seche

Ligne d’eau

Résultats

Tous les positions

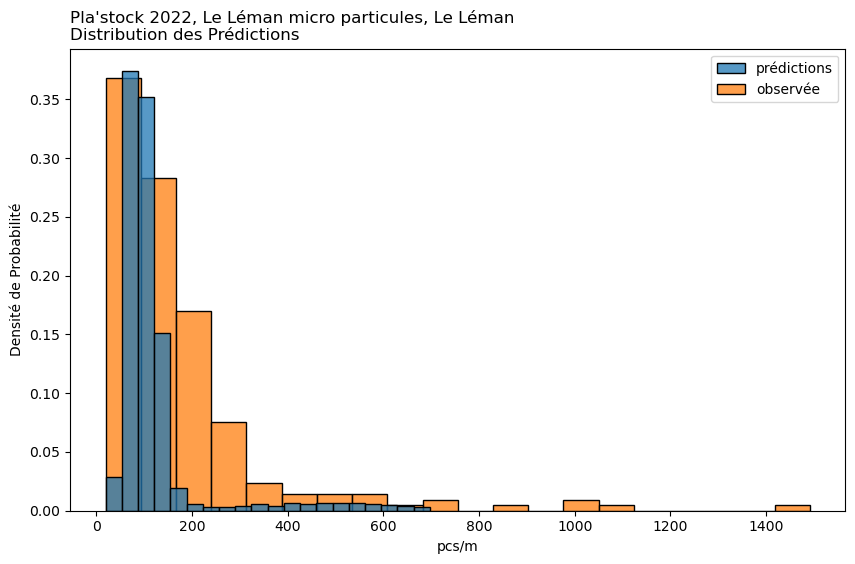
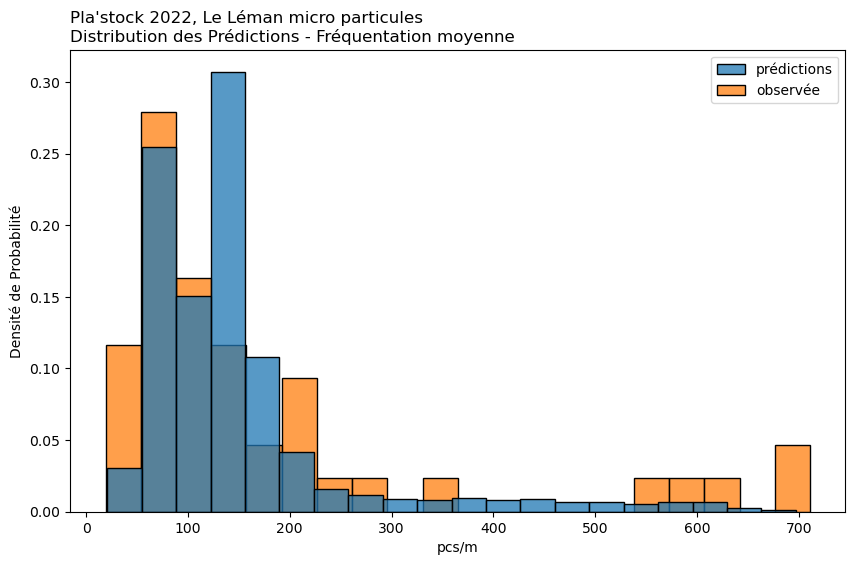
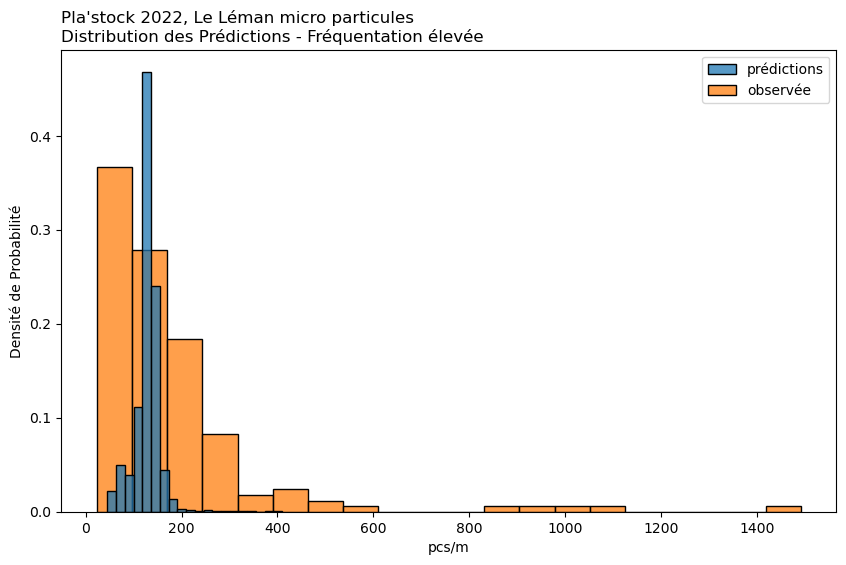
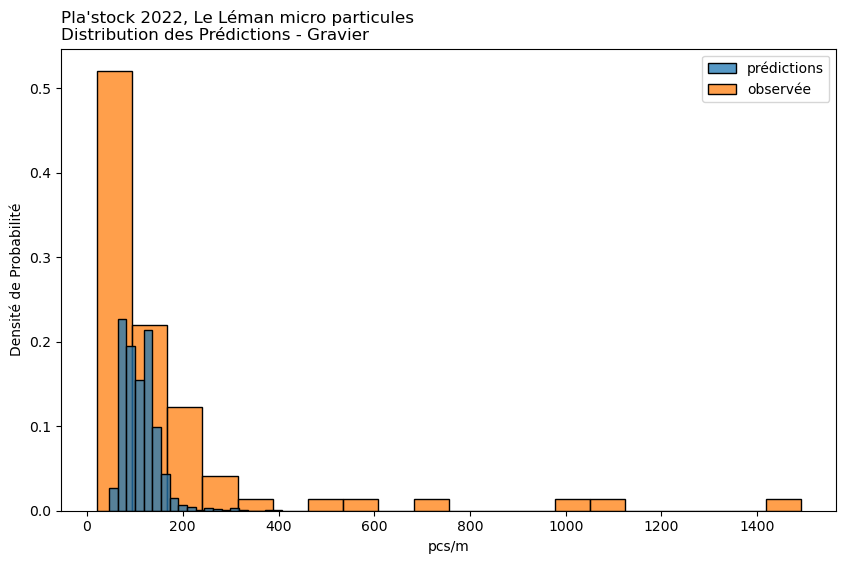
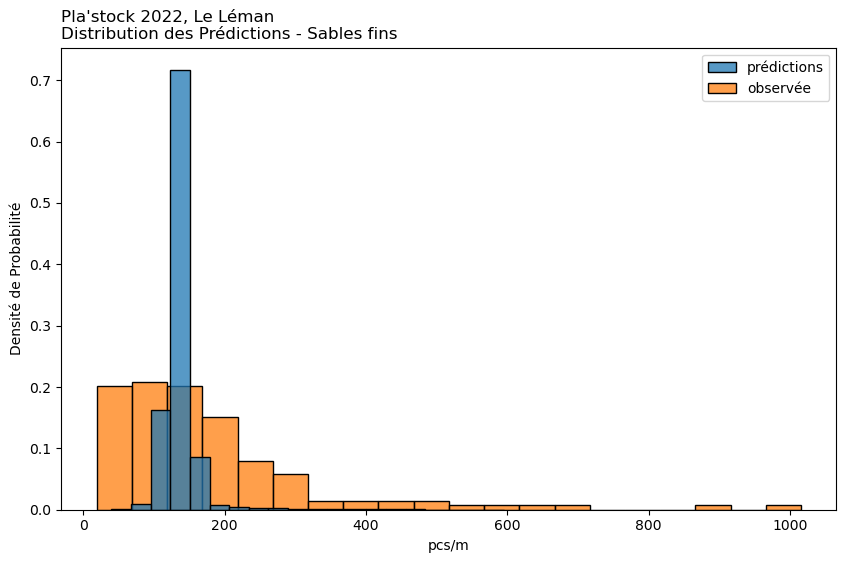
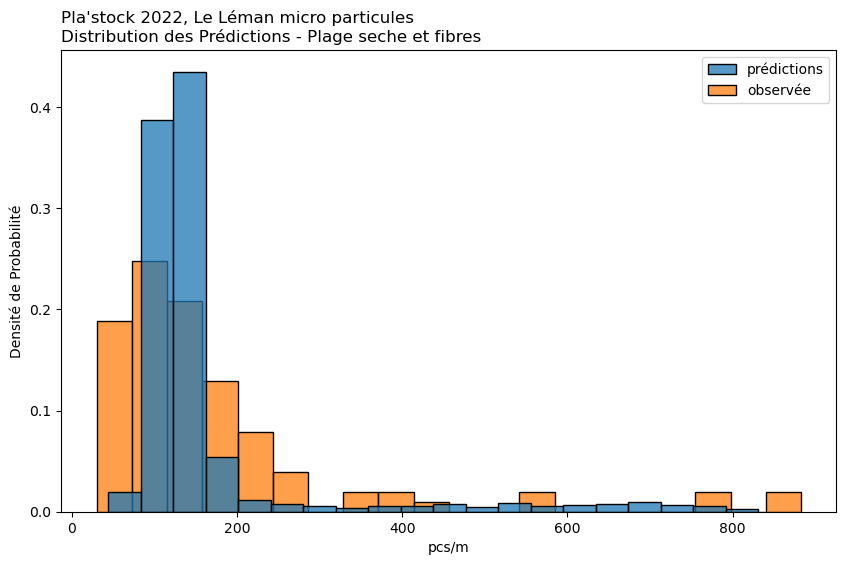
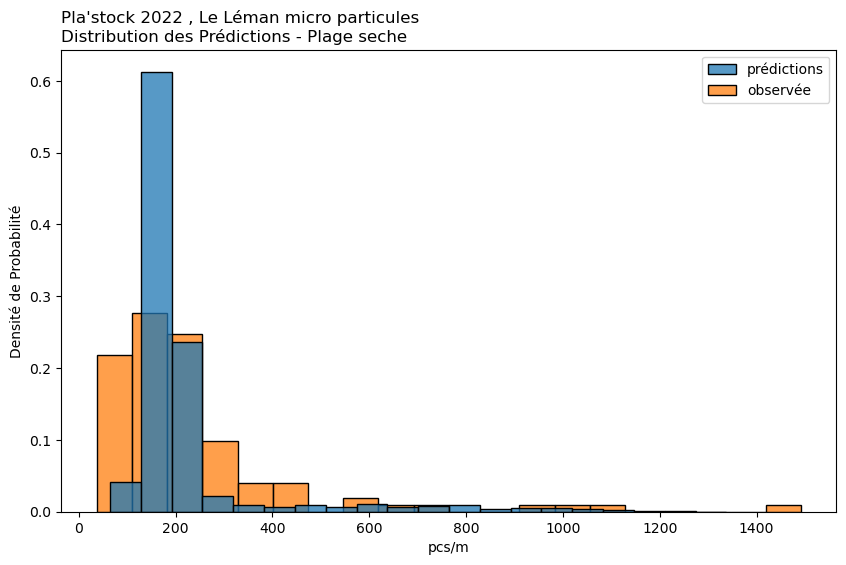
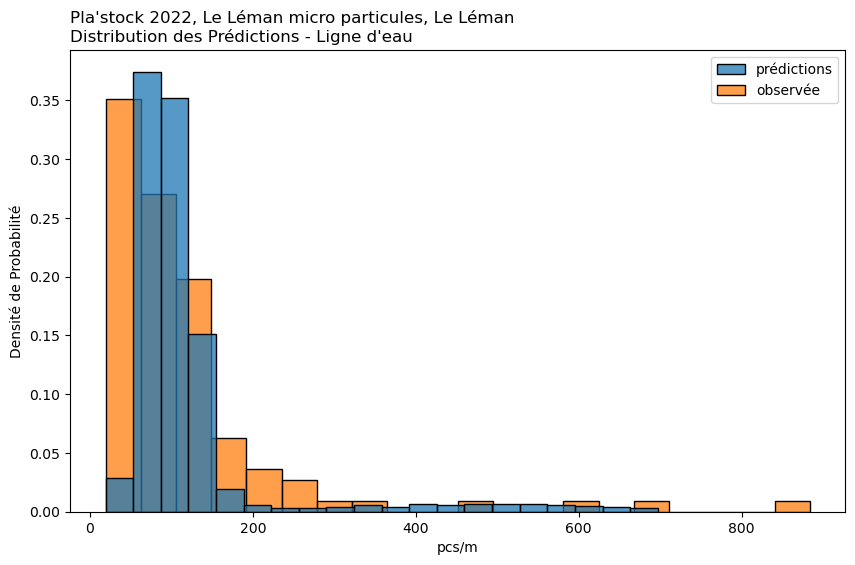
	observée	prédiction
1%	23.22	54.10
25%	71.75	111.90
50%	125.50	135.85
75%	201.75	147.25
99%	1011.71	400.48
Moyenne	175.74	133.50

Ligne d'eau

	observée	prédiction
1%	20.30	44.25
25%	53.50	75.75
50%	85.00	96.80
75%	129.00	120.25
99%	686.80	605.80
Moyenne	116.84	121.69

Fréquentation moyenne

	observée	prédiction
1%	19.42	44.00
25%	63.00	79.30
50%	113.00	128.20
75%	207.00	157.20
99%	705.12	597.86
Moyenne	176.84	148.25

Fréquentation élevée

	observée	prédiction
1%	25.68	58.65
25%	74.00	120.10
50%	128.00	130.05
75%	198.00	139.30
99%	1035.20	197.75
Moyenne	175.46	128.03

Graviers

	observée	prédiction
1%	24.32	57.75
25%	62.00	81.90
50%	90.00	106.40
75%	182.00	128.95
99%	1192.48	250.26
Moyenne	173.03	110.56

Sable

	observée	prédiction
1%	23.76	96.29
25%	84.50	126.54
50%	136.00	134.30
75%	212.00	142.35
99%	812.94	266.10
Moyenne	177.16	137.55

Plage seche et fibres

	observée	prédiction
1%	31.00	74.90
25%	84.00	114.40
50%	124.00	127.60
75%	187.00	148.35
99%	859.00	740.20
Moyenne	175.14	165.82

Plage seche

	observée	prédiction
1%	50.00	99.00
25%	116.00	163.10
50%	185.00	181.10
75%	262.00	201.90
99%	1076.00	977.00
Moyenne	240.47	222.24

Approximation Bayésienne par Grille

Source : solid-waste-team

prior : beta(1,1)

Cas d’utilisation : Cette méthode est une approche manuelle de l’inférence Bayésienne. Elle est particulièrement utile lorsque vous souhaitez incorporer des données antérieures et mettre à jour ces données avec des données observées.

Mise en œuvre : Implique la définition d’une grille de valeurs de paramètres et le calcul de la vraisemblance des données observées à chaque point de cette grille. En multipliant par la probabilité a priori et en normalisant, on obtient la distribution a posteriori. Cela peut être fait pour chaque condition séparément ou pour toutes les conditions ensemble, bien que cela soit plus intensif en termes de calcul.

Toutes les conditions

Fréquentation moyenne

Haute fréquentation

Graviers

Sable

Plage seche et sable fins

Plage seche

Ligne d’eau

Résultats

Toutes les conditions

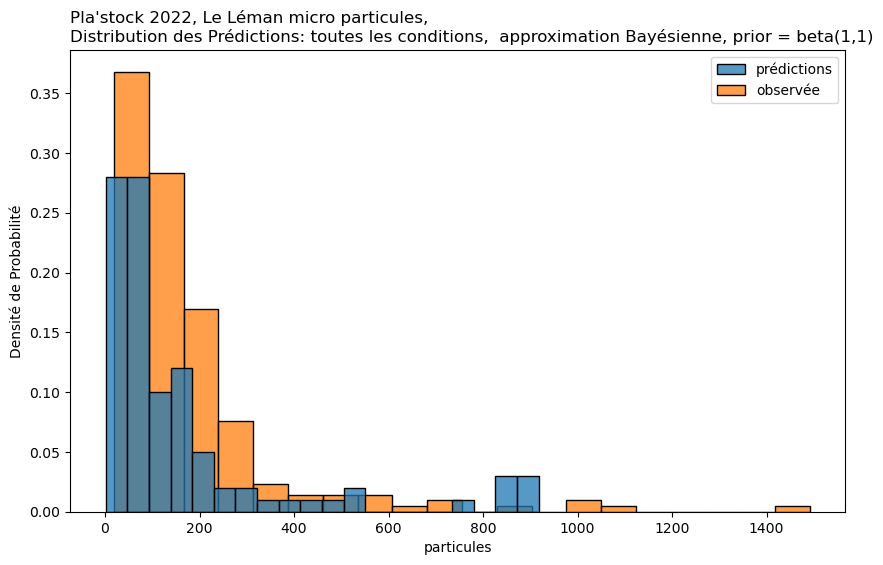
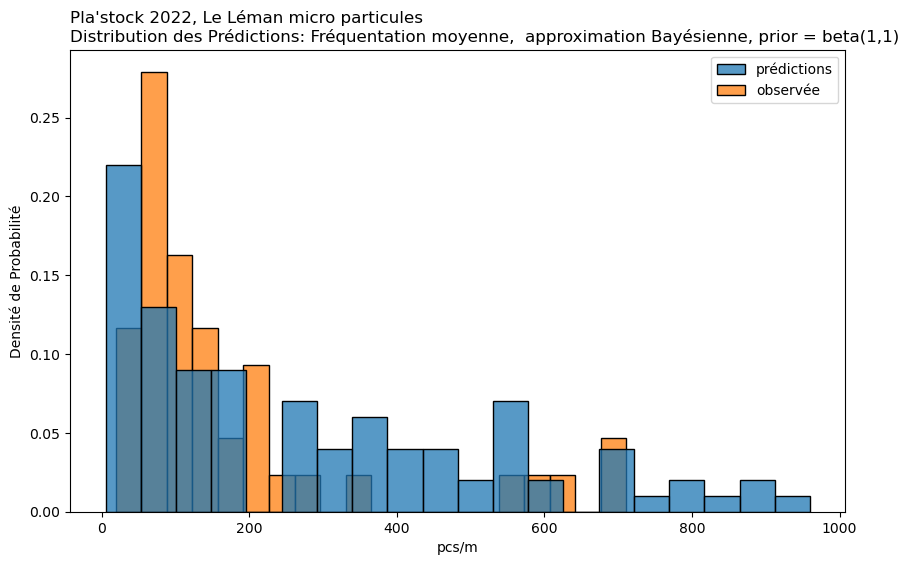
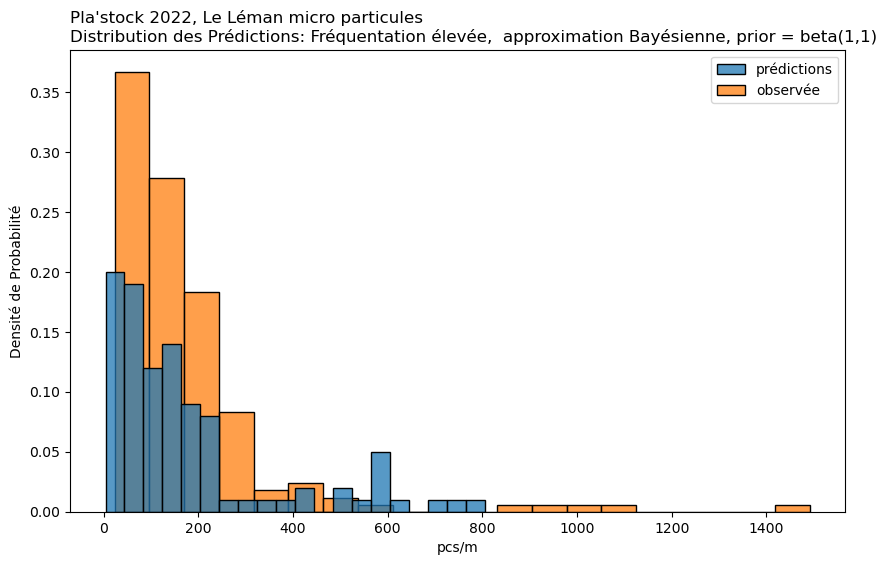
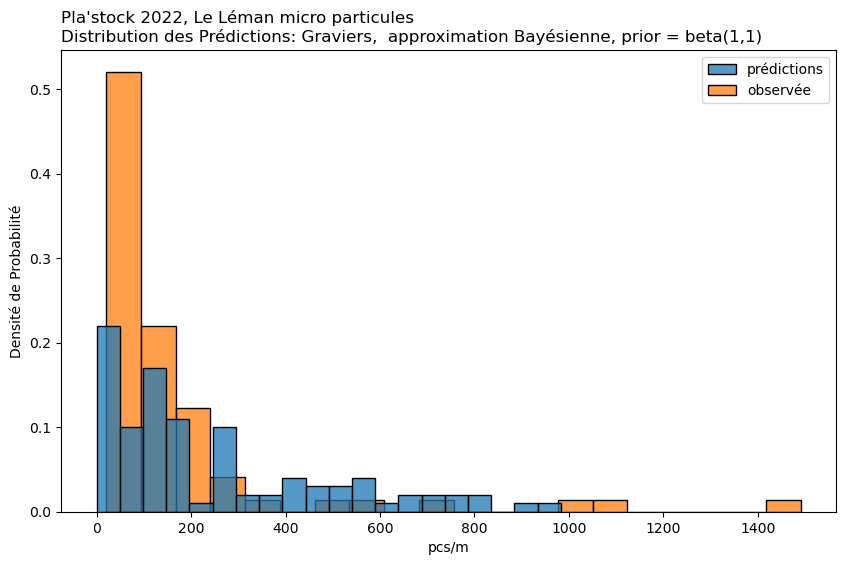
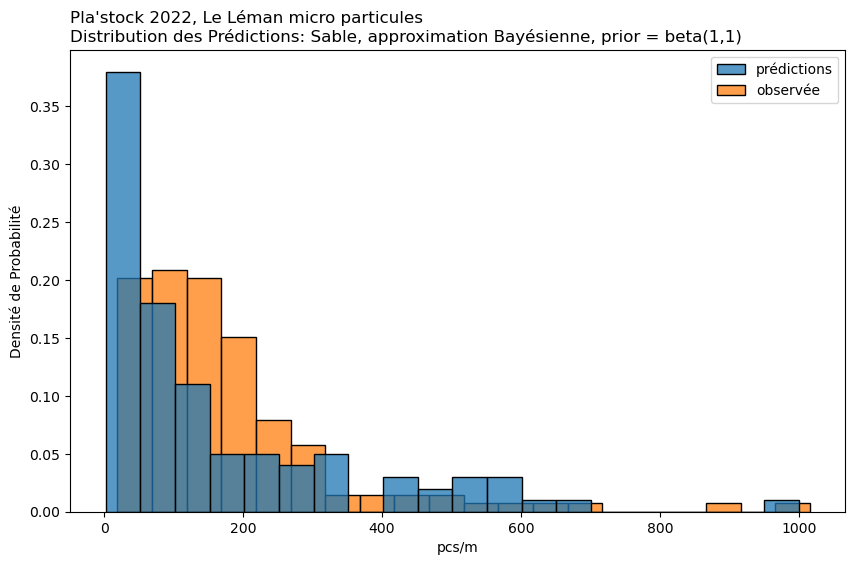
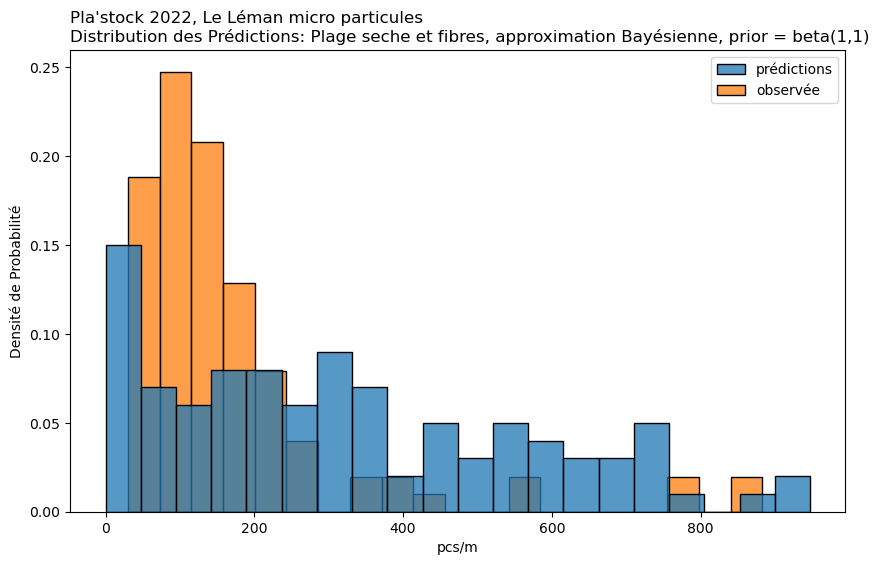
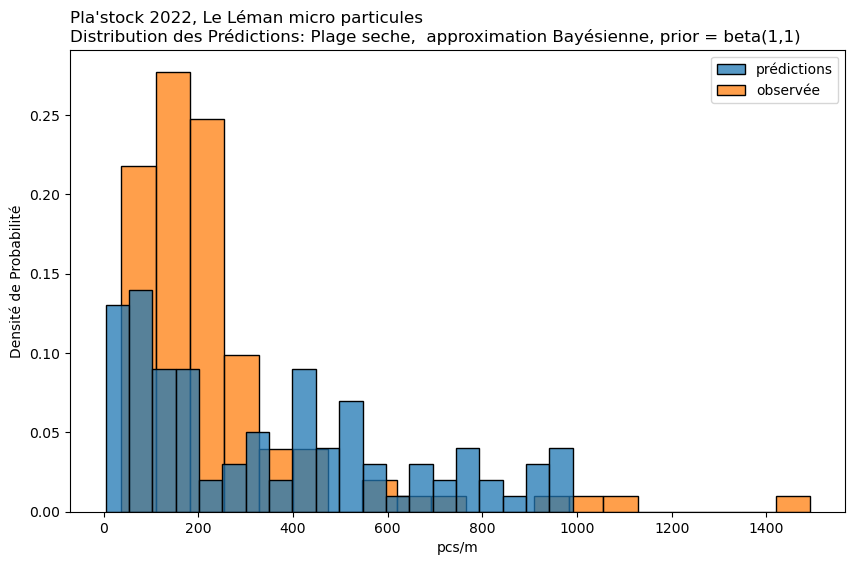
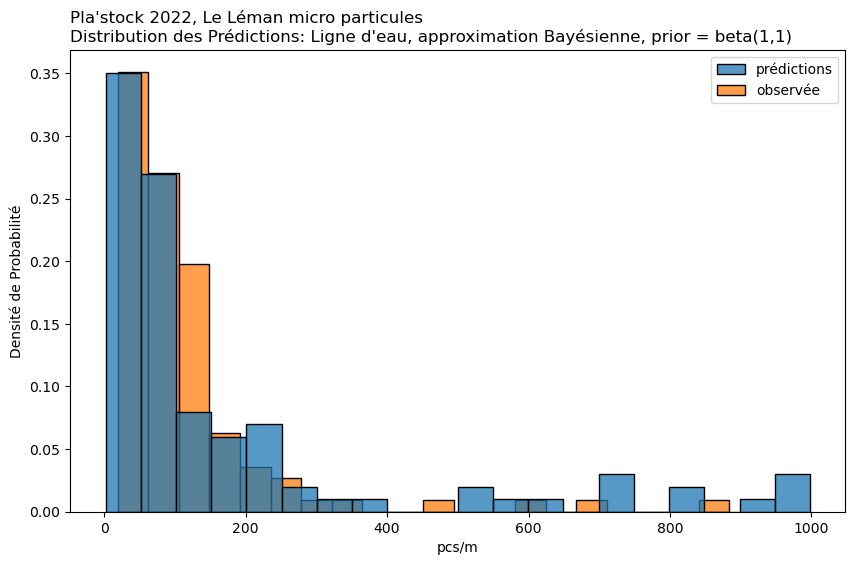
	observée	prédiction
1%	23.22	1.99
25%	71.75	37.00
50%	125.50	77.00
75%	201.75	166.25
99%	1011.71	899.19
Moyenne	175.74	163.72

Ligne d'eau

	observée	prédiction
1%	20.30	2.00
25%	53.50	33.75
50%	85.00	69.00
75%	129.00	181.50
99%	686.80	989.09
Moyenne	116.84	175.91

Fréquentation moyenne

	observée	prédiction
1%	19.42	5.99
25%	63.00	68.00
50%	113.00	182.50
75%	207.00	439.50
99%	705.12	902.58
Moyenne	176.84	278.15

Fréquentation élevée

	observée	prédiction
1%	25.68	5.98
25%	74.00	56.75
50%	128.00	124.00
75%	198.00	210.50
99%	1035.20	746.60
Moyenne	175.46	180.91

Graviers

	observée	prédiction
1%	24.32	0.00
25%	62.00	69.25
50%	90.00	155.50
75%	182.00	396.00
99%	1192.48	887.96
Moyenne	173.03	250.01

Sable

	observée	prédiction
1%	23.76	2.99
25%	84.50	38.00
50%	136.00	80.00
75%	212.00	210.75
99%	812.94	663.40
Moyenne	177.16	162.64

Plage seche et fibres

	observée	prédiction
1%	31.00	10.89
25%	84.00	115.00
50%	124.00	286.50
75%	187.00	493.25
99%	859.00	915.32
Moyenne	175.14	323.05

Plage seche

	observée	prédiction
1%	50.00	4.00
25%	116.00	96.25
50%	185.00	289.50
75%	262.00	520.25
99%	1076.00	975.16
Moyenne	240.47	350.93

Git repo: https://github.com/hammerdirt-analyst/plastock.git

Git branch: jun26

matplotlib: 3.8.2
pandas    : 2.0.3
seaborn   : 0.13.1
numpy     : 1.26.3